2025-01-09 07:42:00
gbragafibra.github.io
This is a brief continuation of a previous post (Repo), which introduced such visualization for collatz sequences based on Langton’s Ant.
Collatz’s Ant is based on the collatz function:
\[f(n) = \begin{cases}
n/2 & \text{if} \quad n \equiv 0 \quad (\text{mod}\, 2) \\
3n + 1 & \text{if} \quad n \equiv 1 \quad (\text{mod}\, 2) \\
\end{cases}\]
and additionally, if $n \equiv 0 \, (\text{mod}\, 2)$ the ant turns 90º clockwise, else the ant turns 90º counter-clockwise. On both accounts, the state of the cell is flipped and the ant moves forward one unit. This is repeated until $n = 1$. An example of such is present in the following animation:

Example of consecutive trajectories from $n = 10^{40}$ to $n = 10^{40} + 20$.

And although this representation is interesting, the flipping of state can eventually lead to ambiguous scenarios where trajectories seem similar to each other through omission.
Given that, the following picture corresponds to the ant’s landscape (final snapshot) without state flipping for the same trajectories, along with respective stopping times. This is done by merely adding a $+1$ count to each coordinate the ant has been through.
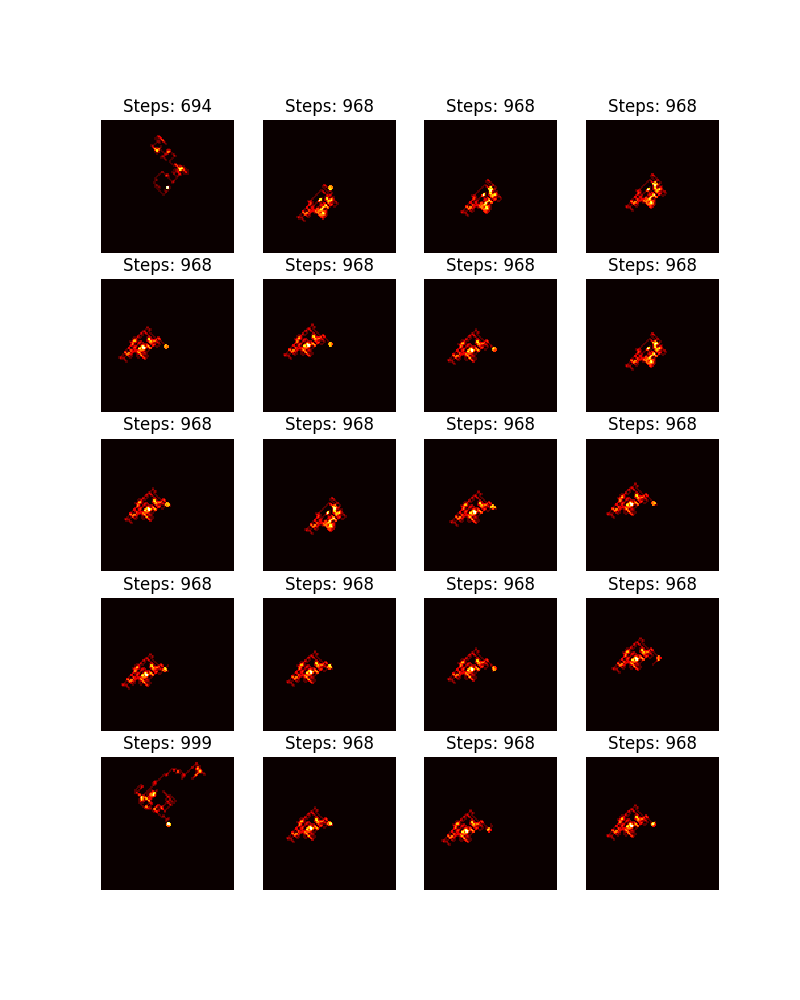
Some other examples
The first 100 numbers from $n = 2$ to $n = 102$.

From $n = 10^{9}$ to $n = 10^{9} + 100$.

From $n = 10^{20}$ to $n = 10^{20} + 100$.
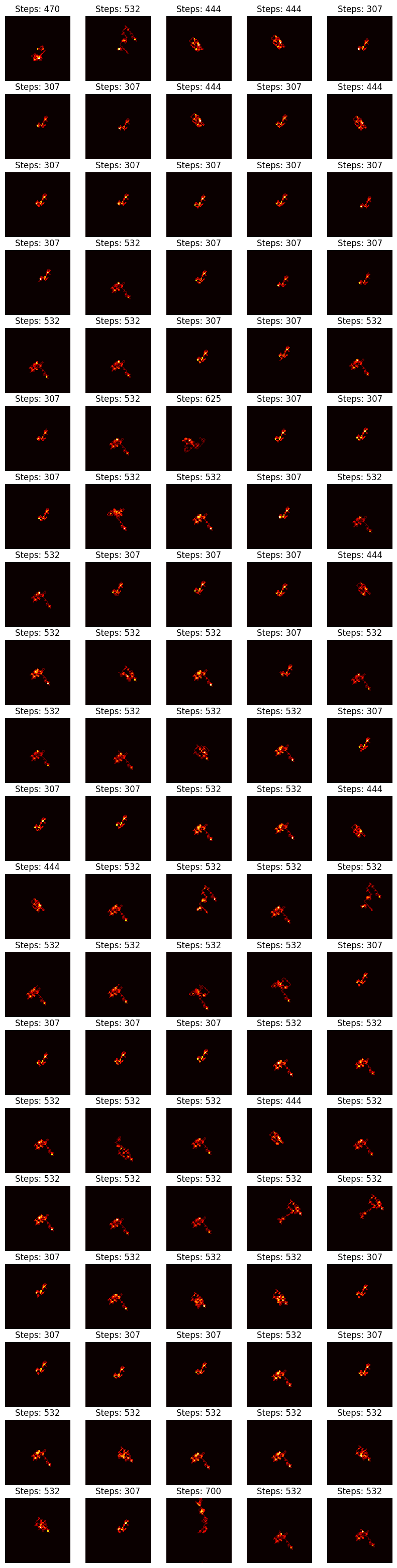
From $n = 10^{200}$ to $n = 10^{200} + 10$.
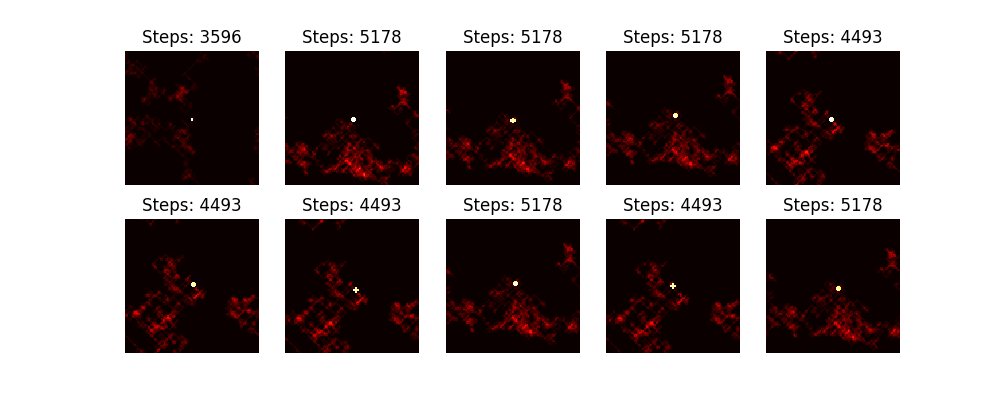
Some interesting things
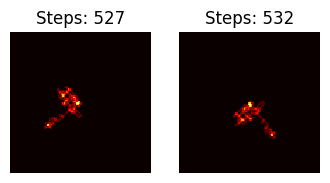
- Very similar landscapes have the same stopping time (or similar ones), but the inverse isn’t true. An example of the inverse not being true, is present in this comparison between $n = 10^{20} + 1$ (1st row, 2nd col) and $n = 10^{20} + 16$ (4th row, 2nd col), both with stopping times 532.
If we check the similarity between both of these trajectories:
import numpy as np
import mpmath
def collatz_seq(n):
seq = []
while n != 1:
seq.append(n)
if n % 2 == 0:
n /= 2
else:
n = 3*n + 1
return seq
mpmath.mp.dps = 22
n1 = mpmath.mpf("1e20") + 1
n2 = mpmath.mpf("1e20") + 16
len(np.intersect1d(collatz_seq(n1), collatz_seq(n2)))
If the same is done between $n = 10^{20} + 16$ and $n = 10^{20} + 20$, which have similar landscapes and the same stopping time, we get:
- Furthermore, if we now look at an example of sub-trajectories converging, in this case with a difference of 5 steps between each, we can see that the landscapes are pretty similar to each other, but for the rotation (which seems to overall be of 90º). This is of course the product of the early re-orientation of the ant given those 5 extra steps.
Example with $n = 18750000000000000004$ and $n = 10^{20} + 16$, the former being found after 5 reduction steps of the latter.
Now with a difference of 100 steps, the landscapes still seem very similar but for a rotation of 180º.

With a difference of 200 steps, the landscapes start losing some detail relative to each other.

And with 300 steps, only a few larger-scale characteristics are now common between the two landscapes.

Keep your files stored safely and securely with the SanDisk 2TB Extreme Portable SSD. With over 69,505 ratings and an impressive 4.6 out of 5 stars, this product has been purchased over 8K+ times in the past month. At only $129.99, this Amazon’s Choice product is a must-have for secure file storage.
Help keep private content private with the included password protection featuring 256-bit AES hardware encryption. Order now for just $129.99 on Amazon!
Support Techcratic
If you find value in Techcratic’s insights and articles, consider supporting us with Bitcoin. Your support helps me, as a solo operator, continue delivering high-quality content while managing all the technical aspects, from server maintenance to blog writing, future updates, and improvements. Support Innovation! Thank you.
Bitcoin Address:
bc1qlszw7elx2qahjwvaryh0tkgg8y68enw30gpvge
Please verify this address before sending funds.
Bitcoin QR Code
Simply scan the QR code below to support Techcratic.

Please read the Privacy and Security Disclaimer on how Techcratic handles your support.
Disclaimer: As an Amazon Associate, Techcratic may earn from qualifying purchases.





























































![[5-Yrs Free Data Recovery] GIGASTONE 256GB SD Card, 4K Camera Pro, A1 V30 SDXC Memory…](https://techcratic.com/wp-content/uploads/2025/09/51F2IcqgHrL._AC_SL1000_-360x180.jpg)



































