The Hashtable Packing Problem

This is part of my project aiming to

1. establish theoretical limits for bitboard based move generation in chess
   and similar games
2. get as close to them as practically possible.

The Hashtable Packing Problem is an optimization problem encountered when
tuning Magic Bitboards in chess. Anyone trying to tackle it will have
suspected
that it is a hard problem, but (to my knowledge) so far no one has bothered
proving that.

But indeed: The abstract Hashtable Packing Problem is strongly
\(\mathcal{NP}\)-complete.
We can therefore stop looking for optimal solutions and instead
use heuristics (and still sleep well).

To follow the proof, no knowledge about chess or Magic Bitboards is required.
A brief discussion about the implications for Magic Bitboards follows at the end.

Definitions

Definition: A Hashtable (for our purposes) is a list of integers
\(\bar{b_0}, b_0, \ldots, \bar{b_i}, b_i, \ldots, \bar{b_n} \).

This means in memory it consists of \(\bar{b_0}\) occupied buckets, followed by
\(b_0\) empty buckets, followed by \(\bar{b_1}\) occupied buckets, and so
on, alternating, ending with \(\bar{b_n}\) occupied buckets.

Now imagine trying to arrange multiple hashtables in memory, possibly
overlapping, while trying to minimize the used space.

Definition: A Hashtable Packing for a list of hashtables
\(B_0, \ldots, B_m\) is a list of integer offsets \(o_0, \ldots, o_m\).

A hashtable packing is valid if none of the occupied buckets overlap, when
building a combined hashtable by placing the hashtables at the given offsets
in memory. That would be a hash
collision for the combined table!

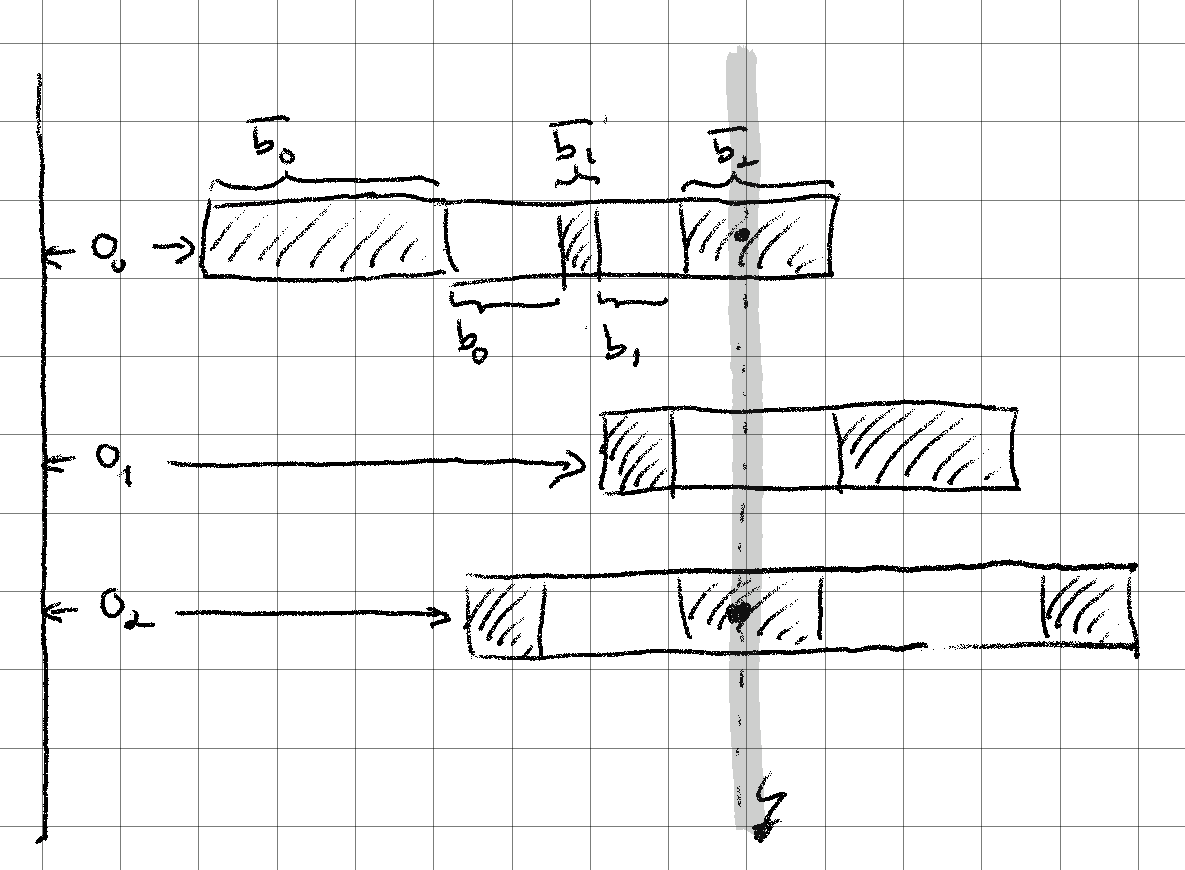
The first occupied bucket of the combined table is at \(\min_{0 \le i \le m} o_i\).
The last occupied bucket of the combined table is at
\(\max_{0 \le i \le m} o_i + \sum_{\hat{b} \in B_i} \hat{b} + \sum_{b \in B_i} b \).
The size of the hashtable packing is the number of buckets that need to be
reserved in memory, including empty buckets between occupied buckets:

$$ 1 + \max_{0 \le i \le m} o_i + \sum_{\hat{b} \in B_i} \hat{b} + \sum_{b \in B_i} b – \min_{0 \le i \le m} o_i $$

Suppose there is an efficient algorithm to solve the optimization problem,
i.e., to find a hashtable packing with minimal size, then there is also
an efficient algorithm to answer the following decision problem.

Hashtable Packing Problem: An instance of the Hashtable Packing Problem
is a list of hashtables and an integer \(K\).

The decision question is: Does there exist a valid hashtable packing for the
given hashtables with size not larger than \(K\)?

Reduction

3-Partition Problem: An instance of the 3-Partition Problem is an integer
\(L\) and a multi-set of integers \(a_0, \ldots, a_n\) with
\(\frac{L}{4} \lt a_i \lt \frac{L}{2}\).

The decision question is: Can the multi-set be partitioned such
that each partition sums to exactly \(L\)?

Observe that the restrictions on the \(a_i\) ensure that each partition would
have to contain 3 elements, which is why this problem is called 3-Partition.
The 3-Partition Problem is known to be strongly \(\mathcal{NP}\)-complete (Garey, Michael R. and David S. Johnson (1979), Computers and Intractability).

Lemma: Hashtable Packing is in \(\mathcal{NP}\).

Proof: We can easily verify in polynomial time that a given hashtable packing is
valid and achieves the desired size.

Lemma: Hashtable Packing is \(\mathcal{NP}\)-hard.

Proof: Let \(L, a_0, \ldots, a_n\) be an instance of 3-Partition.
We construct
a corresponding instance of Hashtable Packing in polynomial time.

First verify basic requirements: \(n\) needs to be divisible by 3, and
\(\sum_{i=0}^{n} a_i = \frac{n}{3}L\). Otherwise return a no-instance.

For each \(a_i\), create one hashtable that simply consists of \(a_i\)
occupied buckets.

Create \(\frac{n}{3}\) identical hashtables
as stencils: \(L+1\) occupied
buckets, followed by \(L\) empty buckets, followed by \(L+1\) occupied
buckets.

Is there a valid hashtable packing for these hashtables with size not greater
than \(K = \frac{n}{3} (3L + 2) \)?

The stencil hashtables are built so that they cannot overlap with each other.
Therefore each stencil contributes \(3L + 2\) to the size of any valid packing.
This means the packing size \(K\) can be achieved if and only if all
remaining hashtables fit in the empty buckets of the stencils, which
each have size \(L\). This is equivalent to the question asked in
3-Partition.

Proposition: Hashtable Packing is strongly \(\mathcal{NP}\)-complete.

Proof: We have already proven \(\mathcal{NP}\)-completeness.

Consider instances of 3-Partition where the largest number (\(L\)) is
restricted by a polynomial in the size of a reasonable (e.g., binary) encoding
of the
instance. Since 3-Partition is strongly NP-complete, the restricted version
remains NP-complete.

Apply the same reduction to create a corresponding instance of
Hashtable Packing. Observe that the largest number (\(K\)) is also
restricted
by a polynomial in the size of a reasonable (e.g., binary) encoding of the
instance.

This means that Hashtable Packing also remains \(\mathcal{NP}\)-complete
under such a restriction, in other words,
the unrestricted Hashtable Packing Problem is strongly \(\mathcal{NP}\)-complete.

Optimal packings for Magic Bitboards

Magic Bitboards
are a technique used to create lookup tables for sliding piece
attacks.
Optimizing Magic Bitboards is a complex intertwined problem:

1. Find candidate magics factors that produce perfect hashtables, at least one
   for each piece type and square.
2. Pick one magic factor for each piece type and square.
3. Find the best possible hashtable packing.

This cannot be solved sequentially, for example the outcome of (3) might
inform the selection made in (2).
Regardless, to decompose this problem, suppose an oracle already revealed the
solutions
for steps (1) and (2) that will lead to an optimal solution.
Even then, the remaining problem is an instance of the
hard Hashtable Packing Problem. For Hashtable Packing we now know that
(due to \(\mathcal{NP}\)-completeness, unless \(\mathcal{P} = \mathcal{NP}\)):

• There is no polynomial-time algorithm to find optimal solutions.

And (due to strong \(\mathcal{NP}\)-completeness, unless \(\mathcal{P} = \mathcal{NP}\)):

• There is no pseudo-polynomial-time algorithm (for example using dynamic
  programming techniques) to find optimal solutions.
• There is no polynomial-time approximation scheme to find optimal solutions,
  i.e., no polynomial-time algorithm that delivers solutions that are
  arbitrarily close to the optimum.
• There is no polynomial-time algorithm to find optimal solutions,
  even when instances are
  encoded with size proportional to the number of buckets
  (e.g., in unary encoding).
  This may be interesting, because unary encoding closely resembles
  the memory representation typically used when validating magic factors.

The instances we are interested in are quite large: Hashtables for
64 rook squares + 64
bishop squares, each with between \(2^4\) and \(2^{12}\) buckets. So
asymptotics are likely to be important!

On the other hand, asymptotic results say nothing about individual instances.
There may even be a restricted set of instances that contains all instances
we care about (including Magic Bitboards in chess), but still can be solved
efficiently.

Then again, the instances we created in the reduction are already quite
restricted: Hashtables have similar size,
and a very limited number of gaps.
The only sources of additional useful
restrictions can be the interaction of (a) the rules of the game
with (b) the particular family of employed hash functions.

We can conclude that an optimal solution cannot efficiently be obtained by
decomposing the problem and abstractly working with the resulting hashtables.
We would have to exploit deeper
connections (if they even exist) between the rules of the game and
mask-multiply-shift hash
functions.

Such insights seem out of reach. At least we now have a good justification
to stop looking for optimality and to employ heuristics
(like Volker Annuss already did successfully).

niklasf, 13th February 2020, discuss on Talkchess.

Keep your files stored safely and securely with the SanDisk 2TB Extreme Portable SSD. With over 69,505 ratings and an impressive 4.6 out of 5 stars, this product has been purchased over 8K+ times in the past month. At only $129.99, this Amazon’s Choice product is a must-have for secure file storage.

Help keep private content private with the included password protection featuring 256-bit AES hardware encryption. Order now for just $129.99 on Amazon!

Help Power Techcratic’s Future – Scan To Support

If Techcratic’s content and insights have helped you, consider giving back by supporting the platform with crypto. Every contribution makes a difference, whether it’s for high-quality content, server maintenance, or future updates. Techcratic is constantly evolving, and your support helps drive that progress.

As a solo operator who wears all the hats, creating content, managing the tech, and running the site, your support allows me to stay focused on delivering valuable resources. Your support keeps everything running smoothly and enables me to continue creating the content you love. I’m deeply grateful for your support, it truly means the world to me! Thank you!